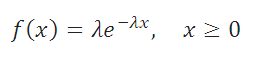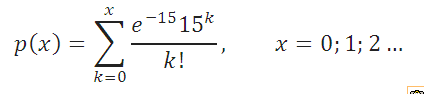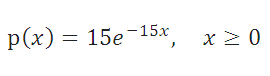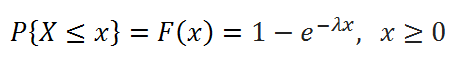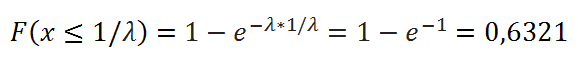Интеграл вероятности



| x | erf(x) | x | erf(x) | x | erf(x) | x | erf(x) |
| 0,000 | 0,0000 | 0,400 | 0,4283 | 1,250 | 0,9229 | 2,250 | 0,9985 |
| 0,020 | 0,0225 | 0,420 | 0,4474 | 1,300 | 0,9340 | 2,300 | 0,9988 |
| 0,040 | 0,0451 | 0,440 | 0,4662 | 1,350 | 0,9437 | 2,350 | 0,9991 |
| 0,060 | 0,0676 | 0,460 | 0,4846 | 1,400 | 0,9522 | 2,400 | 0,9993 |
| 0,080 | 0,0900 | 0,480 | 0,5027 | 1,450 | 0,9597 | 2,450 | 0,9994 |
| 0,100 | 0,1124 | 0,500 | 0,5205 | 1,500 | 0,9661 | 2,500 | 0,9995 |
| 0,120 | 0,1347 | 0,550 | 0,5633 | 1,550 | 0,9716 | 2,550 | 0,9996 |
| 0,140 | 0,1569 | 0,600 | 0,6038 | 1,600 | 0,9763 | 2,600 | 0,9997 |
| 0,160 | 0,1790 | 0,650 | 0,6420 | 1,650 | 0,9803 | 2,650 | 0,9998 |
| 0,180 | 0,2009 | 0,700 | 0,6778 | 1,700 | 0,9837 | 2,700 | 0,9998 |
| 0,200 | 0,2227 | 0,750 | 0,7111 | 1,750 | 0,9866 | 2,750 | 0,9999 |
| 0,220 | 0,2443 | 0,800 | 0,7421 | 1,800 | 0,9890 | 2,800 | 0,9999 |
| 0,240 | 0,2657 | 0,850 | 0,7706 | 1,850 | 0,9911 | 2,850 | 0,9999 |
| 0,260 | 0,2869 | 0,900 | 0,7969 | 1,900 | 0,9927 | 2,900 | 0,9999 |
| 0,280 | 0,3078 | 0,950 | 0,8208 | 1,950 | 0,9941 | 2,950 | 0,9999 |
| 0,300 | 0,3286 | 1,000 | 0,8427 | 2,000 | 0,9953 | 3,000 | 0,9999 |
| 0,320 | 0,3491 | 1,050 | 0,8624 | 2,050 | 0,9962 | ∞ | 1,0000 |
| 0,340 | 0,3693 | 1,100 | 0,8802 | 2,100 | 0,9970 | ||
| 0,360 | 0,3893 | 1,150 | 0,8961 | 2,150 | 0,9976 | ||
| 0,380 | 0,4090 | 1,200 | 0,9103 | 2,200 | 0,9981 |
7.2. Интегральная показательная функция E1(x) = -Ei(-x)
| x | E1(x) | x | E1(x) | x | E1(x) | x | E1(x) |
| 0,010 | 4,037 | 0,078 | 2,050 | 0,560 | 0,493 | 3,40 | 0,00789 |
| 0,012 | 3,857 | 0,080 | 2,026 | 0,580 | 0,473 | 3,60 | 0,00616 |
| 0,014 | 3,705 | 0,082 | 2,004 | 0,600 | 0,454 | 3,80 | 0,00482 |
| 0,016 | 3,573 | 0,084 | 1,982 | 0,620 | 0,436 | 4,00 | 0,00377 |
| 0,018 | 3,458 | 0,086 | 1,960 | 0,640 | 0,419 | 4,20 | 0,00296 |
| 0,020 | 3,354 | 0,088 | 1,939 | 0,660 | 0,403 | 4,40 | 0,00233 |
| 0,022 | 3,261 | 0,090 | 1,918 | 0,680 | 0,388 | 4,60 | 0,00184 |
| 0,024 | 3,176 | 0,092 | 1,898 | 0,700 | 0,373 | 4,80 | 0,00145 |
| 0,026 | 3,098 | 0,094 | 1,879 | 0,720 | 0,359 | 5,00 | 0,00114 |
| 0,028 | 3,026 | 0,096 | 1,859 | 0,740 | 0,346 | 5,20 | 0,00090 |
| 0,030 | 2,959 | 0,098 | 1,841 | 0,760 | 0,334 | 5,40 | 0,00071 |
| 0,032 | 2,896 | 0,100 | 1,822 | 0,780 | 0,322 | 5,60 | 0,00057 |
| 0,034 | 2,837 | 0,120 | 1,659 | 0,80 | 0,310 | 5,80 | 0,00045 |
| 0,036 | 2,782 | 0,140 | 1,524 | 0,82 | 0,299 | 6,00 | 0,00036 |
| 0,038 | 2,730 | 0,160 | 1,409 | 0,84 | 0,289 | 6,20 | 0,00028 |
| 0,040 | 2,681 | 0,180 | 1,309 | 0,86 | 0,279 | 6,40 | 0,00022 |
| 0,042 | 2,634 | 0,200 | 1,222 | 0,88 | 0,269 | 6,60 | 0,00018 |
| 0,044 | 2,589 | 0,220 | 1,145 | 0,90 | 0,260 | 6,80 | 0,00014 |
| 0,046 | 2,547 | 0,240 | 1,076 | 0,92 | 0,251 | 7,0 | 1,15 10 -4 |
| 0,048 | 2,506 | 0,260 | 1,013 | 0,94 | 0,242 | 7,2 | 9,21 10 -5 |
| 0,050 | 2,467 | 0,280 | 0,957 | 0,96 | 0,234 | 7,4 | 7,36 10 -5 |
| 0,052 | 2,430 | 0,300 | 0,905 | 0,98 | 0,226 | 7,6 | 5,88 10 -5 |
| 0,054 | 2,394 | 0,320 | 0,858 | 1,00 | 0,219 | 7,8 | 4,70 10 -5 |
| 0,056 | 2,360 | 0,340 | 0,814 | 1,20 | 0,158 | 8,0 | 3,76 10 -5 |
| 0,058 | 2,327 | 0,360 | 0,774 | 1,40 | 0,116 | 8,2 | 3,01 10 -5 |
| 0,060 | 2,295 | 0,380 | 0,737 | 1,60 | 0,0863 | 8,4 | 2,41 10 -5 |
| 0,062 | 2,264 | 0,400 | 0,702 | 1,80 | 0,0647 | 8,6 | 1,93 10 -5 |
| 0,064 | 2,234 | 0,420 | 0,669 | 2,00 | 0,0489 | 8,8 | 1,55 10 -5 |
| 0,066 | 2,205 | 0,440 | 0,639 | 2,20 | 0,0371 | 9,0 | 1,24 10 -5 |
| 0,068 | 2,177 | 0,460 | 0,611 | 2,40 | 0,0284 | 9,2 | 9,99 10 -6 |
| 0,070 | 2,150 | 0,480 | 0,584 | 2,60 | 0,0218 | 9,4 | 8,02 10 -6 |
| 0,072 | 2,124 | 0,500 | 0,559 | 2,80 | 0,0168 | 9,6 | 6,44 10 -6 |
| 0,074 | 2,099 | 0,520 | 0,536 | 3,00 | 0,0130 | 9,8 | 5,17 10 -6 |
| 0,076 | 2,074 | 0,540 | 0,514 | 3,20 | 0,0101 |
При значениях x
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Самое популярное на сайте:
Формы и системы оплаты труда В современном понимании формы и системы оплаты труда можно определить как организационно-экономические механизмы соотнесения затрат и.
Задания для закрепления. 1. Технологический процесс ремонта представляет собой ________________________ 1. Технологический процесс ремонта представляет собой.
ЧТО ДЕЛАТЬ МУЖЧИНАМ СО СЛАБОЙ ЭРЕКЦИЕЙ Современный последователь учения дао любви Чжан Чжунлань сравнивает импотенцию с простудой — неприятно и раздражает.
Эллинизм. Эллинизм (323-146 до н.э.) стал заключительным этапом древнегреческой культуры Эллинизм (323-146 до н.э.) стал заключительным этапом древнегреческой культуры. Этап эллинизма — начинается с походов Александра.
Условия развития творческих способностей Для развития творчества детям необходимы определенные знания, навыки и умения, способы деятельности, которыми они сами, без помощи.
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .